Credit Migration Framework

This is the first of five articles that provide a high level understanding of the various portfolio models of credit risk covered in the PRMIA syllabus.  Being the first one, this discusses the credit migration framework.  (I am still working on the others.)  This article is intended to provide a conceptual understanding of the approach and I have not provided numerical examples for the reason that I don’t want to duplicate what is already there in the Handbook.  Once you have read this, the scattered explanation in the Handbook will hopefully make more sense.

The credit migration framework is based upon the knowledge of the future distribution of the credit ratings of securities, given a current known rating.  We may know today that a bond is rated say AA, and we know from historical experience (collected and published by all major credit rating agencies) what the likelihood of this bond’s future rating is at the end of one year.  For example, we may know today that the probability of this AA bond moving to a rating of BB is say 4%, and the probability of its staying at AA is 85%.  Now if we know the credit rating of a bond, we also know what it is worth.  How?  Because bond prices for different ratings are observable in the markets.  Based on this information, we can quite easily build a future distribution of an individual bond’s future prices.  Now if we know the correlation between the credit migration (ie, the move from one credit rating to another) of the different bonds in the portfolio, we can generate a distribution of the future value of the portfolio, and thus calculate the portfolio VaR. 
That, in essence, is the credit migration framework.

An individual instrument’s VaR


Let us first consider how Credit VaR for a single bond or instrument is calculated under this approach:
Step 1: Specify the ratings transition matrix to use.  The matrix provides you the observed transition frequencies from one rating to another, and we can use it as ‘probabilities’ for the future transitions across ratings.  These are published by the ratings agencies – you need to pick one.

Step 2: Specify the one year forward zero curve for each rating class (assuming our risk horizon is one year, as is generally the case).  What does a one year forward zero curve mean?  This means the ‘zero curve’ from time = +1 (ie starting at the end of 1 year from now) to future years 1, 2, 3, 4 and so on; so that we can build an interest rate curve that is expected at the end of one year from now.  We will use this interest rate curve to determine the value of the bond at the end of 1 year from now for each of the possible credit ratings it can assume in the future.  Note that there will be a different curve for each rating class.  Each curve will be applied to the coupons and final payment on the bond to determine its PV at the end of year 1 from now.

Step 3: Using the probabilities from the transition matrix in Step 1, and the possible future bond values from Step 2, we get a distribution of future values of the bond.  Note that if we know the possible future values of the bond, and the probability of its actually being at that value, we can quite easily calculate an expected value, or average.  But that is not the point.  What we want is the distribution so we can get our bottom 1% or 5%, or whatever level of confidence we are interested in as VaR.

Let me expand on one nuance in Step 2 on establishing bond values.  Assuming you know the different rates for the different years, you calculate the value of the bond by discounting the future cash flows to the present.  

For example for a 4 year bond, this might look like:

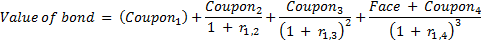
Question is – in the last term, what value do you use for the bond’s face or notional value?  Generally, it would be $100, or whatever the nominal value of the bond is.  But when the rating category to which a bond moves is “D” or default, the value to be discounted will be the recovery value.  The recovery value will depend upon the distribution for the recovery rate, introducing this additional complexity which is addressed by using Monte Carlo simulations when considering default.

So far so good – we know what the bond will be worth at the end of the year if

• we know what rating it is in, and
• our transition matrix from one of the rating agencies gives us the probability of its being in a particular rating.

This gives us the future distribution of the bond’s value, and once we have that, it is quite easy to come with the VaR estimate by just drawing a line at the 99th, 95th or other percentile that we are interested in as the level of confidence.

Getting to portfolio VaR

This is all very good and easy, but unfortunately things don’t stay this simple.  The reason is that while the above logic is quite easy to apply to a single bond, things get complex where there are many bonds in the portfolio.  It is straightforward to calculate the individual VaRs of the bonds as above, but combining them to calculate the portfolio VaR can be quite challenging.  This is because the probabilities of credit migration (ie the move of the bond from AA to any other rating, including staying as AA) of the different bonds in the portfolio are not independent.  They are correlated.  If one AA bond migrates to being BBB at the end of one year, the likelihood of the credit downgrade of the other bonds goes up.  (You might like to read the article on default correlations, a very related concept.)  This relationship is tricky and difficult to incorporate into combining the individual credit VaRs for the credit VaR for the portfolio.  

The question now is how do we combine these distributions together to get the distribution for the portfolio’s value as to be able to get our portfolio VaR?  Combining them is not just a matter of adding up individual VaRs because as I just mentioned, the distributions are correlated to each other; ie if one bond goes down, the possibility of others in its class and even others going down goes up.  If these were normal distributions, one could combine them as multivariate normal distributions – which are essentially separate normal distributions connected together by their correlation.  But the distributions of future bond values aren’t normal distributions either.

Let me take a small digression to remind you a bit about multivariate normal distributions.  This is going to come in handy in a moment.  A normal distribution is defined by its mean and standard deviation.  Two correlated normally distributed variables have what is called a bivariate normal distribution.  If you graph it, it is a 3D graph – the wireframe variety with x and y on the two horizontal axes and z representing probability on the vertical z axis.  (Look at the end of this tutorial for bivariate normal distributions.)  The shape of the wireframe for the bivariate normal distribution is determined by the correlation between the two variables.  (A bivariate distribution is one possible multivariate distribution – a bivariate distribution has by definition 2 variables, while a multivariate distribution may have many more.)

A multivariate distribution with more than two variables is difficult to show graphically as we would need more than 3 dimensions, and is a computationally difficult task to build the distribution’s pdf as the covariance matrix becomes unwieldy fairly quickly.

Regardless of the difficulty of graphing or calculating, given correlations between the variables we can calculate the area under the curve below a certain level of confidence for a multivariate distribution, thereby obtaining the VaR.  How the credit migration approach does it is that it uses return correlations to generate correlated asset returns in a Monte Carlo simulation (using Cholesky decomposition), and calculates the VaR.

Wait a second you might say – the last sentence makes no sense.  Till a minute ago we were talking in an abstract sort of way about correlations between rating migrations, and suddenly we have introduced asset returns and return correlations. Let me explain that.

At this point, the Credit Migration framework makes a couple of big leaps of reasoning:

1. The ratings for a firm are a function of its asset returns – because when the firm’s assets fall below a certain level, default will occur.  In a similar way when assets fall below other levels, credit migration to lower credit ratings will occur too.
2. Asset returns are normally distributed.  If we take this normal distribution of asset returns and slice it in a way that each slice has area under the curve equal to the migration probabilities, we can determine how many standard deviations away from the mean do returns on the firm’s assets need to be to hit a certain rating.  (Let us call it the ‘sliced normal distribution’ for the time being.) For example, if a firm has assets of $100, and debt of $60, the firm needs to make a loss of more than $40 to default on the debt.  If the standard deviation of asset returns is $15, then we need to have a -2.33 standard deviation returns to hit default.  In the same way, the ‘thresholds’ for other credit ratings can also be calculated.
3. Asset returns cannot be directly observed.  Not a problem.  We can use stock returns to proxy asset returns.
4. Correlations between asset returns of different firms cannot be observed.  Not a problem, another assumption to the rescue. We can assume that stock returns are a proxy for asset return correlations.

All of the above reasoning certainly does assume a lot.  You can pick a lot of holes in the reasoning above (eg, the firm may be financed by debt as well as equity, equity returns do not necessarily mirror asset returns nor they may be normally distributed, and the correlations between equity returns may not mirror the correlations between ratings migration, nor would they be very stable.  (But while you can do that, I would suggest we move on and keep preparing for the exam.)

Calculating area under a multivariate normal distribution can be computationally challenging, with thousands of bonds in the portfolio (refer the last item under distributions for finance for an example of the bivariate normal distribution.  Therefore the credit migration approach uses Monte Carlo simulation to generate returns scenarios.

At this point, what we know is:

1. Standardized return thresholds for each rating class for each of the bonds in the portfolio, ie if we know the asset returns for a bond issuer, we can say what the future credit rating would be (using the sliced normal distribution).  The ‘thresholds’ are the points where a crossover from one rating to another happens.
2. We know the correlation between the asset returns of the different issuers (calculated from stock price returns).
3. We know the one year forward zero curve for different rating classes, so we can value the bonds given a future bond rating.

With this information, this is what we do for calculating the portfolio risk:

1. Generate scenarios for asset returns using the return correlations that we know, assuming all returns are jointly normally distributed.  (Correlated variables can be generated using Cholesky decomposition that you studied in Exam 2.)
2. Each scenario gives us the actual return for each issuer, from which we predict the future credit rating of the issuer’s bond using our sliced normal distributions explained above.
3. Using the one year forward zero curves, we calculate the value of each bond for that one scenario, and add them up to get the value of the portfolio.  This gives us one observation for a simulated future portfolio value.
4. We do these steps 1-3 above lots of times – say 100,000 times – and get a distribution of future portfolio values.

Now that we have the distribution after step 4 above, we can calculate the VaR of the portfolio.  Problem solved!

That is all that there is to it.