If you are new to finance, or haven’t actually done much math in a while, the differences between discrete, compounded and continuously compounded interest rates can be quite confusing. You may go through many chapters in the handbook while still having a nagging doubt as to if you really get the interest rate part – sometimes they use (1+r)^n, at other times it is exp(rn), what’s going on? This brief article explains what continuously compounded interest rates are, how they work and how they are to be used.
Rates come in two varieties: simple interest, and compound interest. Simple interest means you earn a rate of interest on the principal, and that is it. The principal never increases due to interest being added to it. Compound interest, as we remember from high school, compounds the interest periodically. Continuously compounded interest is an extreme case where the compounding frequency approaches infinity.
We should be able to convert from one rate type to another, as this is often needed for a number of calculations across many subjects. This tutorial in particular looks at continuously compounded rates as
Simple interest calculations are very straightforward, but rarely used in practice in finance. For the rest of this discussion, we use the following notation:
– FV be the future value of a deposit,
– PV its present value (or principal),
– r the nominal annual interest rate,
– t the time
– m the compounding frequency per year and
– n the number of periods (also equal to t*m), then:
Using simple interest, FV = PV x (1 + rt)
When using compound interest, the interest is periodically added to the principal at intervals determined by the compounding frequency. If the compounding frequency is m, then:
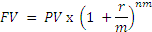
So if the frequency of compounding is 2, and the nominal rate is 5%, a deposit of $100 will grow to
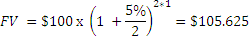
As we keep on increasing the compounding frequency, we will find that the future value of the deposit will keep on increasing as interest earned gets to work earlier and the deposit starts earning more money on the interest sooner. But the increase in the final future value is not infinite, no matter how high the compounding frequency is. As the compounding frequency rises to infinity, the FV approaches an amount equal to ert, where e is the base of the natural logarithm. (What ‘e’ signifies is not relevant for the PRM exam, but what is relevant for us is to remember that ert can be evaluated in Excel using the function EXP, so ert= EXP(rt).
FV = ert
What is the continuously compounded rate of return if we know prices?
Continuously compounded rates of return are also called ‘log returns’. If S2 is the price at the end of a period, and S1 the price in the beginning, then:
Return based on simple interest = S2/S1 – 1
Continuously compounded return = ln(S2/S1), where ln is the logarithmic function.
(In Excel, the function is called exactly that – ie LN, and you can calculate logarithmic returns in Excel using the formula =LN(S2/S1))
Annual effective rate and continuously compounded rates
Annual effective rate, also called the “APY” (annual percentage yield) in the United States, is a standardized way of expressing rates with different nominal rates and compounding frequencies. It is a way of expressing any given interest rate in terms of the equivalent simple interest rate for one year. For example, for a CD paying a rate of 5% annually compounded every six months, the annual effective rate is 5.625%.
If we know the annual effective rate, we can calculate the continuously compounded returns as
Continuously compounded rate = ln(1 + Annual effective rate)
Similarly, Annual effective rate = exp(continuously compounded rate) – 1
Continuously compounded rates are much easier to deal with. For example, if an investment earned 2% in one period and 3% in the next period, the total return is (1 + 2%) x (1 + 3%) – 1. However, if these were continuously compounded rates, we could just add the returns to mean 5%. This follows from the property of logarithmic functions that continuously compounded rates are.
Remember the following with reference to continuously compounded rates:
- FV=PV x ert = exp(rt)
- PV=FV x e-rt = exp(-rt). This intuitively follows from the equation for FV because PVs are just the same as FVs with negative time elapsed.
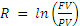 , where FV is future value (for example, a price at the end of a period) and PV is the present value (for example, a current price)
, where FV is future value (for example, a price at the end of a period) and PV is the present value (for example, a current price)

Your comment is awaiting moderation.
Hey there, I think your blog might be having browser compatibility issues. When I look at your blog in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, great blog!