This is the fourth of five articles covering each of the main portfolio approaches to credit risk as explained in the handbook. The idea is to provide a high level and concise explanation of each of the approaches so it may be easier to deal with the detail provided in the handbook. I hope you find it useful.
The KMV approach follows the same logic as the structural approach to a point, ie, the firm defaults when the value of assets falls below a certain level. But as an end product, it comes up with the expected default frequency (EDF) (ie the probability of default). Much of the workings of the KMV approach are proprietary and available only to KMV customers, and we need to focus on a conceptual understanding of the approach.
Similar to what was explained for the structural approach, default happens when the value of assets falls below a certain value, called the ‘default point’. (The ‘default point’ under KMV is not the same as the point where the value of the assets falls below the value of the total debt.) Over time, the assets of the firm will earn a certain return and trend with a given mean and volatility. Under KMV, the value of the firm’s assets is assumed to be log-normally distributed, ie the returns on the assets are normally distributed.
There are essentially three steps to the credit risk assessment process under the KMV approach:
Step 1: Determine the value of assets (V) and their volatility (σ)
The value of equity (as represented by the stock price, S) is driven by:
- Value of the firm’s assets (V)
- The volatility of the assets (σ)
- The leverage ratio (L)
- The coupon on long term debt (c) and
- The risk-free rate (r)
Of the above, the last three are known variables, and so is the stock price. The only unknown variables are V and σ. The volatility of the assets is not the same as the volatility of the stock price, as the latter is driven by the value of the assets. KMV uses an iterative approach to find out V and σ, given a knowledge of the S, L, c and r.
Step 2: Calculate the ‘distance to default’ (DD)
A key concept underlying the KMV approach is the recognition that a firm does not have to default the moment its asset value falls below the face value of debt – in fact default happens when value of the firm’s assets falls somewhere between the value of the short term debt and the value of the total debt. In other words, it is possible to not have default even if the value of the assets has fallen to less than the total debt. This is natural because it is generally the current cash needs (driven by short term debt) that cause default – the firm may have enough cash to keep paying all liabilities as they come due even though the total liabilities may be greater than the total assets.
KMV sets the default point as somewhere between short term debt (STD) and the total debt as the total of the short term debt and half the value of the long term debt.
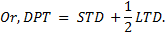
Next, the KMV approach determines what the ‘distance-to-default’ is. The distance to default is the number of standard deviations assets have to lose before getting to the default point (DPT). It is calculated as follows:
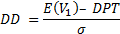
Where σ is the standard deviation of future asset returns. Each of the terms in the equation above are explained below:

This can be expressed another way – as a multiple of the standard deviation of the expected returns.
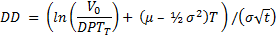
where μ and σ are the mean and volatility of the asset returns.
[How did we get from the first equation to the other?Kzg,You are right, as I read it, it does look like a leap of faith from one equation to the next. Here is an explanation, hope this helps.The formulas are practically identical. Think of the first equation as being expressed in absolute dollar terms, ie, the numerator E(V1) – DPT represents the dollar value that needs to be lost to hit the default point. Dividing that by the standard deviation (in dollars) gives you the number of standard deviations away you are from the default point.For the second equation, think of measuring the same distance-to-default in terms of returns measured not in dollars but in percentages (continuously compounded).Assume for a moment that the default point, DPT = $100, and the current value of assets, V0 = $120. Therefore during the next year we can afford to lose:(a) $20, expressed as a percentage return (of the DPT), plus(b) Whatever we will earn in the coming year (as a percentage).The $20 when expressed as a continuously compounded return in terms of log returns is ln($120/$100) (about 18%), or =ln(V0/DPT). To this we need to add what we will earn what we will earn in the coming year. That number is μ, or to be precise μ – (σ^2)/2, because volatility reduces continuously compounded returns. (See separate tutorial here that explains how volatility kills returns, though for short periods the adjustment of “– (σ^2)/2” isn’t really needed. http://www.riskprep.com/all-tutorials/35-exam-1/129-volatility-returns-and-stock-prices).So the numerator ends up being [ln(V0/DPT) + (μ – (σ^2)/2)T]The denominator would be σ, which in its more pure form is expressed as σ√T just in case σ is for a different time period than the one under consideration. (WHich is also why μ – (σ^2)/2 ends up getting multiplied by T.)Thus the distance to default can be expressed asDD = [ln(V0/DPT) + (μ – (σ^2)/2)] / σ√TThink of the first equation as being expressed in absolute dollar terms, ie, the numerator E(V1) – DPT represents the dollar value that needs to be lost to hit the default point. Dividing that by the standard deviation (in dollars) gives you the number of standard deviations away you are from the default point.For the second equation, think of measuring the same distance-to-default in terms of returns measured not in dollars but in percentages (continuously compounded).Assume for a moment that the default point, DPT = $100, and the current value of assets, V0 = $120. Therefore during the next year we can afford to lose:(a) $20, expressed as a percentage return (of the DPT), plus(b) Whatever we will earn in the coming year (as a percentage).The $20 when expressed as a continuously compounded return in terms of log returns is ln($120/$100) (about 18%), or =ln(V0/DPT). To this we need to add what we will earn what we will earn in the coming year. That number is μ, or to be precise μ – (σ^2)/2, because volatility reduces continuously compounded returns. (See separate tutorial here that explains how volatility kills returns, though for short periods the adjustment of “– (σ^2)/2” isn’t really needed. http://www.riskprep.com/all-tutorials/3 … ock-prices).So the numerator ends up being [ln(V0/DPT) + (μ – (σ^2)/2)T]The denominator would be σ, which in its more pure form is expressed as σ√T just in case σ is for a different time period than the one under consideration. (WHich is also why μ – (σ^2)/2 ends up getting multiplied by T.)Thus the distance to default can be expressed asDD = [ln(V0/DPT) + (μ – (σ^2)/2)] / σ√T ]
Step 3: Determination of the EDFs
The last step is the determination of the expected default frequencies – which is a mapping of the distance-to-default to probabilities of default based upon a proprietary database (provided to customers using the ‘Credit Monitor’ service).
Based upon what was explained in 2 above, EDFs are affected by:
- Stock price
- Leverage ratio and
- Asset volatility.
That is about all there is to the KMV approach for the exam!
