This is the third of five articles covering credit risk – this one addresses the ‘structural approach’.
The CreditMetrics approach treats all issuers in a particular rating class as the same without considering the unique financial characteristics (such as recovery rates) for each issuer. The rating itself is a synonym for default rates, ie a particular expected default rate puts an issuer in a particular rating class.
The ‘structural’ approach is markedly different and follows the following argument:
- A firm (ie the issuer) is financed by debt and equity, and the total of these two is equal to the assets of the firm (ie, the ‘balance sheet’ view where the liability side (debt and equity) is equal to the asset side.)
- The firm will default when the value of the assets fall below the value of the debt. If the value of the assets of the firm falls below the value of the debt, the owners of the firm (ie the equity holders) can walk away from the debt by handing over the assets of the firm to the debtholders in full settlement.
- In other words, economically speaking the equity holders have a right to ‘sell’ the assets of the firm to the debtholders at a price equal to the face value of the debt. Of course, so long as the value of the assets stays above the face value of the debt, they will not exercise this right as they can keep the surplus for themselves. But if the value of the assets falls below the value of the debt, they will ‘sell’ these assets to the debtholders at an amount equal to the face value of the debt.
- In other words, the equity holders have a long put position on the assets of the firm. The debtholders have sold them this option. In this ‘option’,
- the exercise price is the face value of the debt,
- the assets of the firm represent the underlying, and
- the current value of the assets is the ‘spot’ price in the option
- the exercise date of the option is equal to the date the debt is to be paid back
- If the debtholders had not provided this put option to the equity holders, they would have had a risk-free asset.
- The ‘price’ of the put is reflected in the price at which the debtholders acquired the debt. So for a speculative grade issuer, the put is valuable and the debt trades at a discount that reflects the default rate. For a high quality issuer, the put may be worth far less, and that is reflected in the debt trading at near risk-free rates.
- In other words, Risky Loan + Put on Assets = Risk-free Loan. (Why? Because the Risky Loan includes a short position in the put, and by buying the same put, the short put position embedded in the risky loan is offset).
- The value of the ‘Put on the Assets’ represents the credit risk from the issuer.
- The value of the put on the assets can be calculated using Black Scholes. Since this is a Put, and we know what the value of a put is according to Black Scholes (refer here for a quick review), we can say that the value of this put is equal to:
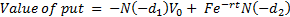
Two key terms in the formula above clarified:
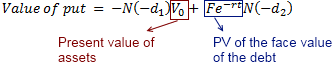
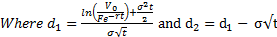
In this model:
- Credit risk increases as the volatility of the assets (σ) increases
- Credit risk increases as t, the time to the repayment of the debt, goes up.
- Credit risk increases as r, the risk-free rate, goes down.
The credit risk for any issuer is reflected in its spreads, ie the difference between the yield on the issuer’s debt and risk-free debt issued by the treasury.
This default spread is a function of three predictable things:
- The leverage ratio (ie the issuer’s debt/equity ratio)
- The volatility of the underlying’s assets
- Debt maturity
Structural approach in action: an example
Consider a 1 year bond that has a face value of F and a current market price (or PV) of B. Thus the return on the bond is F/B – 1.
Now assume the value of the put is P. The put together with the bond constitute a risk-free portfolio. Therefore F/(B+P) – 1 = r, where r is the risk free rate.
In the real world, we know F, we know B and we know r. Therefore we can calculate P or the value of the put from this relationship. In reality, what we are saying is that if we know what the current price of a risk-free bond, and the price of our risky bond, then the difference between the two represents the credit risk or the value of the put.
How does any of the above really help in risk management if we can’t really buy a put on the assets of the firm?
The answer is that while we can’t buy a put on the assets of the firm, we can construct a ‘synthetic put’ on the same. How?
The logic works as follows:
- The delta of a put is N(–d1). So we can construct a synthetic put by shorting N(–d1) of the assets of the firm. (Note that this synthetic put will be valid only for small local movements around the current prices – and will need to be readjusted often.)
- But you can’t really short any assets of the firm. All we have available to us are the shares of the firm that are traded publicly.
- A small digression: The option that the equity holders have. If you have followed how the debtholders have sold a put option on the firm’s assets to the equity holders, here is an alternative way to think about it:
- The equity holders have the right to take all the assets of the firm by paying the debtholders an amount equal to the face value of the debt. If they believe the assets of the firm are more valuable than the amount payable to the debtholders, they will exercise this right, otherwise not. In other words, the equity holders have a call option on the assets of the firm, where the exercise price is equal to the face value of the debt.
- The value of this call option is the value of equity. This can be written as (again, refer to the value of a call under Black Scholes)
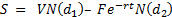
- In other words, the publicly traded shares of the company represent a call option on the assets of the firm. The very same assets that we need to short to create our synthetic put. The delta of this call option is N(d1).
- Since we want to sell short –N(–d1) units of the assets, and the call option that equity represents on these assets has a delta of N(d1), therefore by selling short –N(–d1)/N(d1) units of the shares we can get our synthetic put option that creates the short position in the company’s assets of N(–d1) units.
That really is about it to the structural approach.
