First and second derivatives are important in finance – in particular in measuring risk for fixed income and options. In fixed income – the first and second derivatives are modified duration and convexity respectively, and for options, these are delta and gamma. But what do these really mean – and what does one think about them when one sees a number? The rest of this article attempts to provide an intuitive look at how price changes for a bond (or an option) are determined by the first and the second derivative, what they mean, and how they are to be interpreted.
Note that this isn’t a repetition of the text book – though some of that is inevitable. The idea is to provide an intuitive understanding of what these variables are, what they really represent, and how to think about them.
What this article will cover is as follows:
- the first derivative – modified duration or delta; and the second derivative – convexity or gamma
- how they are useful in estimated changes to the price of an instrument
- how does the Taylor expansion using these make sense
- and how to think when you see a number. For example, if the convexity of a bond is 200, what does that really mean? Is it good or bad? If it is good, how good is it?
To keep the discussion grounded in reality, let us start with bond pricing. I am going to use a rather exaggerated example with large round numbers just to make it easier to follow.
The linkage between bond prices and yields is not linear – and that is because the bond yield – the ‘r’ in the equation, appears in the denominator of the formula for a bond’s price. Recall that a bond’s price is the present value of its future coupons and final payment. This gives us the familiar convex curve that links bond yields to price. (Quick diversion: what does a ‘convex’ curve mean? It means that if you take any two points on a curve and join them by a straight line, the curve lies below such a straight line. Between those two points, the curve is considered convex. Conversely, a concave curve will lie above the line joining the two points.)
Think of the graph below. Think that we are moving from yield Y1 to Y2. As a result, the price moves from P1 to P2. Now Y1 and Y2 are percentages. Say yields are moving from 3% to 5%. Ie, Y1 is 3% and Y2 is 5%. Assume as a result the price of the bond moved from $100 to $80. This means that the price moved by $20 for a 2% change in yield. Or $10 for 1% change in yield. Now “$10” is not a very useful way to express the price change, because to be able to place $10 in perspective we will need to know the initial value of the bond, or the value of portfolio in case we are doing these calculations for a portfolio. Therefore we express the $10 change as a percentage. In this case, the percentage is $10/$100 = 10%. 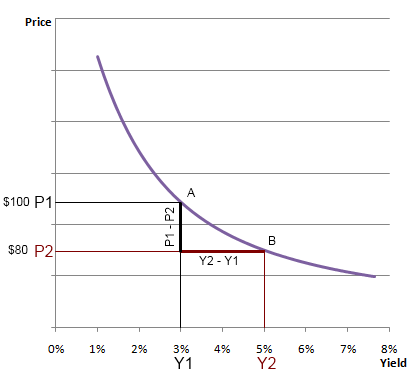
Based on this illustration, we can say that the bond price moves by 10% for a 1% change in yield. This is the modified duration. It is just the rate of change. Formulaically, we can express the rate of change as
![]()
Note that I am not yet calling the first derivative as modified duration. (This is because the numerator is still absolute dollars, and the sign is not yet accurate.)
Just to keep life simple, let us say that ![]() (as a percentage), and let
(as a percentage), and let ![]() .
.
Because P1>P2, ΔP is a +ve number. And because Y2>Y1, ΔY is a –ve number. Therefore the ratio ΔP/ΔY will be a negative number. For reasons of convention, we ignore the negative sign because we know that for bonds yields going up would mean prices going down, and therefore putting the minus sign is redundant.![]()
The numerator of this ratio is a number without any units, just a percentage reflecting the change in price. The denominator is the yield. Therefore the ‘units’ modified duration is expressed in is ‘change in price per unit of yield’. So when we say that the modified duration of a bond is 10, we mean that a x% change in yield will lead to a 10*x% change in price.
Intuitively, it is easy to understand if we were to say that a modified duration of 10 means that a 1% change in yield will cause a 10% change in price. This is great for an elevator discussion, and for internalizing what to make of a modified duration number.
Actually this is not exactly true. A 1% change in yield is a fairly large change. What we mean really by modified duration is the effect on price for a very small change in yield. The small change in yield could be Δx. Modified duration is another way of saying that for a Δx change in yield, the price will change by MD* Δx.
What happens if Δx becomes very large? Does this simple relationship (ie, price will change by MD* Δx) still hold? Well, only upto a point. As Δx starts becoming larger, MD starts changing too. So to go back to our example to yields changing from Y1 to Y2, if we could break down the move of rates from Y1 to Y2 to lots of small Δxs, we would see that at every step the MD is slightly different from the previous one. We could get an approximation of the price change using just the MD and multiplying it by ΔY, but we could do better if we can take into account the fact that the MD itself has changed during the move from Y1 to Y2.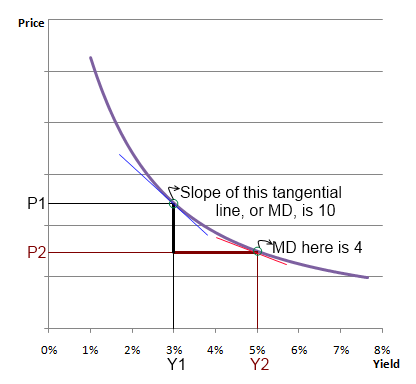
But what about the ‘rate of change’ of the modified duration itself? Assume for a moment that the modified duration at point Y1 is 10. But as we move from Y1 to Y2, MD starts decreasing. By the time we get to Y2, MD has come down to 4 (hypothetical). So as we estimate the price change based on a rate change from Y1 to Y2, which MD should we use? The MD at point Y1 (which is 10), or the MD at point Y2 (which is 4)?
The answer to this question is somewhere roughly in the middle would be a reasonable approximation. In other words, something close to 7. Note that this is fairly intuitive – we just took the middle point of the two MDs to be a fair linear approximation.
If you are still with me, great. Now let us talk about how we can use the second derivative to arrive at the MD of “7” which we thought was intuitively a better number to use than either 10 or 4. The second derivative represents the ‘rate of change’ of the modified duration. How much does the MD change as a result of the yield move from Y1 to Y2? Very straightforward – it has declined by 6 (=10 – 4). Now Y1 was 3% and Y2 was 5%. So for a 2% move in interest rates, modified duration has reduced by 6. Can we express this in terms of a regular 1% move in yields? Sure. We can say that for a 1% move in yield, the modified duration reduces by 3 (=6/2). This is the rate of change of modified duration.
This is what convexity is from a conceptual perspective – though not from a formula point of view (we will get there in a second).
Now think about it for a minute – convexity represents the rate of change of modified duration. Modified duration itself is the rate of change in price in response to a change in yield. Substituting, we can say convexity represents the rate of change of the rate of change in price in response to a change in yield. That sounds very complex, but in reality that is what it is. The second derivative is the rate of change of the first derivative. But we prefer to say it in the first simpler easier to understand way – ie, convexity reflects the rate of change of modified duration.
With the above intuitive understanding, let us calculate convexity. Convexity can be defined as ΔMD/ΔY – ie the change in MD divided by the change in yield. Now MD itself = ΔP/ΔY.
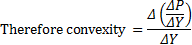
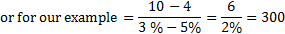
That looks really simple. My convexity is 300. But what do I make of this number? So let us look at the units of each of the numbers so we can see what is going on.![]()
The units of the numerator are ‘PriceChange% / Yield%’. The units of the denominator are just ‘Yield%’. Therefore the units of convexity are ‘PriceChange% / Yield%2’. Now that is not quite easy to interpret – because of the square term in the denominator.
Let us see how we interpret modified duration. Modified duration is the percentage change in price from a 1% change in yield. So if modified duration is 10, we can say that a 1% change in yield leads to a 10*1% = 10% change in price. Extending the analogy, convexity is then the change in modified duration from a 1% change in yield. So if convexity is 300, we can say that a 1% change in yield leads to a change of 300*1% = 3 in modified duration. See what is happening with the units here
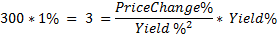
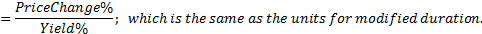
So by multiplying the convexity with our unit of yield change (ie 1%), we get the change to modified duration.
What is the effect on price from convexity? We multiply by Yield% one more time, and get the change in price. No different really from what we would do with modified duration.
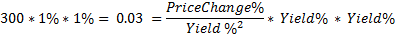
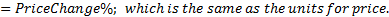
What this means is that a convexity of 300 means a 1% change in yield will lead to a 3% (0.03) change in price resulting from convexity – in addition to the change in price resulting from the modified duration. In other words, the convexity adjustment to the price will be over and above what the modified duration suggests as the price change, and therefore including convexity improves our estimates of price changes from changes in yield.
Now we come back to our original example. Yields change from 3% to 5%, and as a result modified duration changes from 10 to 4. Now what is the effect on price? Recall we had said that intuitively the ‘right’ duration to use as rates move from Y1 to Y2 would be something in between, ie 7? Now let us look at how we can get to this 7 if we know duration and convexity at point Y1 (3%).
If modified duration is 10, and convexity is 300, what is the effect of a change in yield from 3% to 5% on a bond’s price? Looking at just the first derivative, the answer will be = Modified duration * 2% = -10 * 2% = 20%. But we know that as we move from 3% to 5%, the modified duration does not stay constant at 10 during this entire range, and we should adjust for that fact. How much do we adjust? The modified duration at 3% would be too high, that at 5% be too low, and somewhere in between is just right. If convexity is 300, then by the time the rates go from 3% to 5% the modified duration would have moved by 300 * 2%. We should take half of that as the adjustment.
That is, the modified duration we should use is ![]() . In other words,
. In other words,![]() . Since this is the new improved modified duration, in order to see the change in price, we should multiply it by the change in yield, ΔY.
. Since this is the new improved modified duration, in order to see the change in price, we should multiply it by the change in yield, ΔY.
Or, ![]()
![]()
This is nothing but the Taylor expansion that you would find in text books as being the explanation as to how to get to changes in bond prices from a change in yield. You can get a fairly good estimate of a change in a bond’s price by using only the first term in the expression above. That will be a first order estimate. You can improve the estimate by including the second term as well.
Hope the above explanation helps internalize something about modified duration and convexity.
To summarize:
- To interpret a modified duration number, think of it being the percent change in value from a 1% change in yields. It is the first derivative of the price with respect to yield. Because prices and yields move in different directions, the first derivative is negative. Modified duration however skips the minus sign as a convention.
- To interpret a convexity number, think of it as being the percent change in modified duration from a 1% change in yield. To estimate what the effect of including convexity in a price change calculation for a 1% change in yield, multiply the convexity by 1%^2=1%*1%.
If you think about it, convexity reflects the error in the estimation of a bond’s price if modified duration alone were to be used in such an estimate. You fix part of that by using the rate of change of the first derivative. (Actually, you could go on. Even convexity does not stay constant over a range. You could account for the rate of change of convexity – by using the third derivative! But that would be quite pointless.)
Another basic point – one might say that hey, I already know the bond pricing formula, I can just calculate P1 and P2 and get the exact change in price to the nth decimal place. I don’t need to do any approximations and mess with convexity and modified duration. That is a fair point if you are only looking at one bond. When you have a large portfolio of say thousands of bonds (consider the Lehman or now Barclays Global Aggregate), then this full calculation of each bond’s price becomes too intensive an exercise. It is easier to calculate the duration of the portfolio, and its convexity, and estimate price changes and risk using these rather than a full computation.
Options: Delta and Gamma
Delta and gamma are the first and second derivatives for an option. If S be the price of the underlying, and ΔS be a change in the same, then the value of the option is given by V(S + ΔS) = V(S) + ΔS x delta + 0.5 x gamma x (ΔS)2.
Note how similar the whole thing is in structure to what we discussed for bonds. You can apply exactly the same logic as for bonds – delta is the first derivative, and gamma the second.

Your comment is awaiting moderation.
Good post however I was wanting to know if you could write a litte more on this subject? I’d be very grateful if you could elaborate a little bit further. Bless you!