In this article we will discuss basic vanilla options, calls and puts, and understand payoff diagrams. We will also look at the put-call parity. The put-call parity is important to understand for the PRMIA exam as a number of questions, such as those relating to the relationship between call and put values, the additive nature of option Greeks is based upon the put-call parity.
Payoff diagrams
There are two types of options – calls and puts. In the rest of the discussion below, I refer to ‘stocks’, but we could really be talking about any security, for example an FX position, a bond, or a commodity.Also, for constructing these payoff diagrams I have ignored option premiums so we can focus on the payout.Option premiums can be considered constants that move the entire graph up or down, without changing its shape which is what we are interested in.
Payoff for a stock position
The payoff for a stock position is linear.The payoff increases or decreases linearly with price, depending upon whether it is a long or a short position.
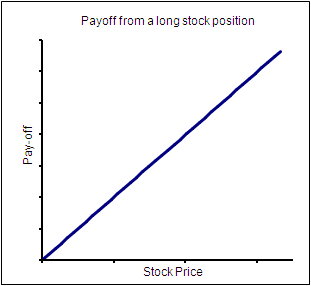
The payoff from a short stock position is just the opposite:

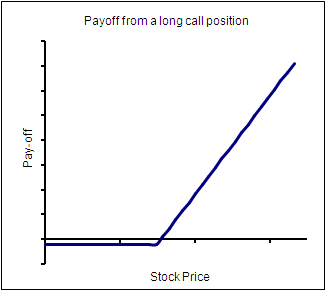
A long position in a call option has a zero pay off till the exercise price, after which its payoff is identical to that of the stock.(When creating the payoff diagrams below, we have ignored the premiums paid, which are a constant amount and therefore merely move the payoff graph up or down in the ‘parallel’ sense.)
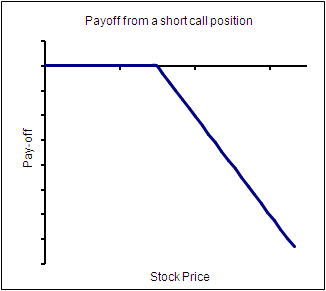
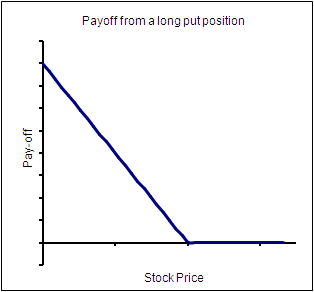
The payoffs for a short call, a long put and a short put are given below:

How to remember what different payoff diagrams look like:
Here is a simple trick that some may find useful to remember what option payoff diagrams look like.The one pay-off diagram you will need to remember is the long call.Recall that this looks as follows:

To get the short call pay-off diagram, assume there is an imaginary mirror placed on the x-axis.The reflection of the ‘long’ payoff in this imaginary mirror will be the pay-off of the short position.This applies to every option position, or complex set of positions.To visualize the payoff of a short (or a long) position given the long (or the short) position’s payoff, place an imaginary mirror along the x-axis and flip the pay-off line.
To get the long put position from the long call, imagine there is a mirror along the y-axis this time.You get the pay-off from a long put position.Given this, you can visualize the payoff from a short put position too.
Combining payoffs
Complex options positions can be understood by combining payoff diagrams.Next, we will combine payoff diagrams to understand the put-call parity.
Understanding put-call parity
Imagine an options portfolio with a long call and a short put position, both with the same exercise price.This will have the following payoff:

Compare the resulting payoff – the diagram on the right hand side.This looks just like the payoff for the stock, except that the line is a bit lower.And it is lower by exactly the amount of the exercise price, present valued to today.
By combining a long call with a short put, we end up with a linear payoff, just like for the stock.This linear payoff, combined with a bank deposit, has a payoff identical to a stock:

Combining the two, we get:
Call – Put = Spot – PV of exercise price
This is the put-call parity. Notice the right hand side of this equation. The exercise price is a constant, and so is the spot price.So at any point in time, RHS is fixed. This means Call – Put, the LHS, is fixed too. Therefore if call prices rise, put prices would rise need to rise too in order to maintain the parity.
This can also be written as:
Spot + Put = Exercise price x e-rt + Call
Note the notation – “Call – Put” can be written as “Long Call + Short Put”.The minus sign indicates a short position.
So we can write the put call parity as:
Long Call + Short Put = Spot Price + Bank Borrowing
You can expect questions that draw upon your knowledge of the put-call parity in the PRMIA exam.
