This rather brief article covers some familiar theory – how are options valued – but without repeating all the text you can find in a textbook. Of course, we all know about the Black Scholes model, and anyone can punch it into Excel or use any number of online calculators available for free. What this article tries to do is to provide an intuitive understanding of what drives option values, and also provides an Excel model incorporating the Black Scholes that you could use to play around with.
Consider an American option to buy an IBM share at $50, when the current spot price is $80. Clearly, the option has a value of $30 inherent in it, something called ‘intrinsic value’. The option will not sell for less than $30. In fact, the option has some time to run till maturity, creating additional possible upside for those who wish to hold the stock. The option will sell for something more than $30, though we don’t know exactly how much more.
Consider an American call with a strike close to the spot price. It will have the payoff  . What would its value be at any point in time? Two observations can be made about the option’s value:
. What would its value be at any point in time? Two observations can be made about the option’s value:
1. The option cannot be more valuable than the stock itself. Why would one pay more for an option to buy a stock than the stock itself? Even if the exercise price is very attractive, say as low as being close to zero, it will still make no sense to pay more than the value of the stock itself.
2. The option cannot be lower than the profit that can be made by exercising the option right now. If it were to be lower, it would offer the possibility of riskless profits, something that would disappear in less than an instant in the markets.
Therefore the value of the stock is an upper bound for the value of the option, and the intrinsic value represents a lower bound to the value of the option. The actual value of the option would lie somewhere between these two bounds, as shown below
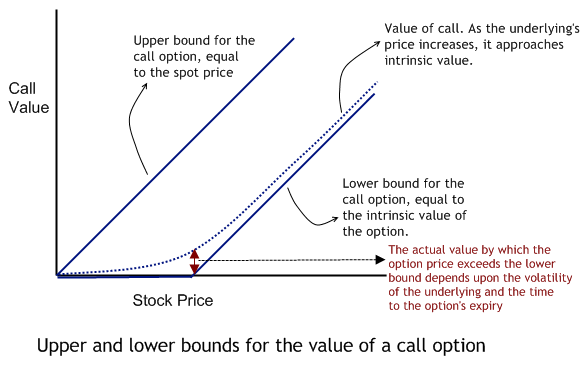
Factors affecting the call option’s price
Consider an extreme case where the option is so deep in-the-money that it is certain to be exercised. In that case, holding the option is almost equivalent to holding the stock itself. If we were to exercise the option right now, it would mean an immediate outflow equal to the exercise price, something that can be postponed till the expiry date. So even if nothing more, by not exercising the option we are saving interest on the exercise price till the expiry date of the option. The option therefore has to be at least equal to the risk free interest on the exercise price from now till the expiry date.
It is easy to intuit from here that an increase in interest rates will increase the value of the option. So will an increase in the time to expiry. Buying a call that is certain to be exercised is the equivalent of buying a share on credit, and therefore the value of this call will depend upon the time to expiry and the interest rate.
Ignoring dividends, the price of a call is related to:
1. Price of the underlying
2. Exercise price
3. Interest rate
4. Time to expiry
5. Volatility of the underlying
Options are riskier than the underlying. How much more risky are they really? The answer to this question depends upon whether how much in or out-of-the-money they are. Options deep in-the-money or deep out-of-the-money are less risky than an option at-the-money. The value of the option can change quite a bit as the price of the underlying fluctuates around the exercise price. The riskiness of an option therefore varies with changes in the price of the underlying (becoming less risky as it moves away from the exercise price). It is also affected by the time to expiry. The greater the time to expiry, the greater is the risk. This is easy to comprehend if we consider a limiting case where the option is very close to expiry. At this time, the price of the underlying is unlikely to change much, and the payoff from the option is almost certain. Similarly, the risk of the option also depends upon the risk of the underlying. The more volatile the underlying, the greater is the volatility of the option. One outcome of the varying risk of an option is that we cannot use discounted cash flow analysis to value it as the discount rate would vary based upon risk, which itself is changing.
The Black-Scholes formula for option valuation
The Black-Scholes formula for option valuation uses five parameters to provide a value for an option. For the PRMIA exam, we do not need to go into how the BSM is derived, nor do we need to remember the formula.
Here is a spreadsheet that models the Black-Scholes – have a look, and try out a few values. The spreadsheet actually has a custom function (called ‘bs’ – no witty comments please!). Enter the five parameters, and see the call and put values on the right, together with the Greeks.
